반응형
#include <stdio.h>
#include <stdlib.h>
// Function to merge an array
// with l(left), m(middle), r(right) index
void Merge(int arr[], int l, int m, int r)
{
int i, j, k;
// Sizes of arrays
int n1 = m-l+1; // l ~ m
int n2 = r-m; // m+1 ~ r
// Copy data to temp array L[] and R[]
int L[n1];
int R[n2];
for(i=0 ; i<n1 ; i++)
L[i] = arr[l+i];
for(j=0 ; j<n2 ; j++)
R[j] = arr[(m+1)+j];
i = 0; // Initial index of L
j = 0; // Initial index of R
k = l; // Initial index of merged array
while(i <= n1-1 && j <= n2-1)
{
if(L[i] < R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// When there are any elements in L
while(i <= n1-1)
{
arr[k] = L[i];
i++;
k++;
}
// When there are any elements in R
while(j <= n2-1)
{
arr[k] = R[j];
j++;
k++;
}
}
// Function to sort an array using merge sort
void MergeSort(int arr[], int l, int r)
{
// for left index == right index ( an array with one element )
if(l < r)
{
int m = (l+r)/2;
MergeSort(arr, l, m);
MergeSort(arr, m+1, r);
Merge(arr, l, m, r);
}
}
/* Function to print an array */
void PrintArray(int arr[], int size)
{
printf("\n********************************\n");
for(int i=0 ; i<size ; i++)
{
printf("%4d", arr[i]);
}
}
// Driver program to test above functions
int main()
{
int array[7];
for(int i=0 ; i<7 ; i++)
{
printf("Put your %d integers : ", i);
scanf("%d", array+i);
}
int n = sizeof(array)/sizeof(array[0]);
PrintArray(array, n);
MergeSort(array, 0, n-1);
PrintArray(array, n);
return 0;
}
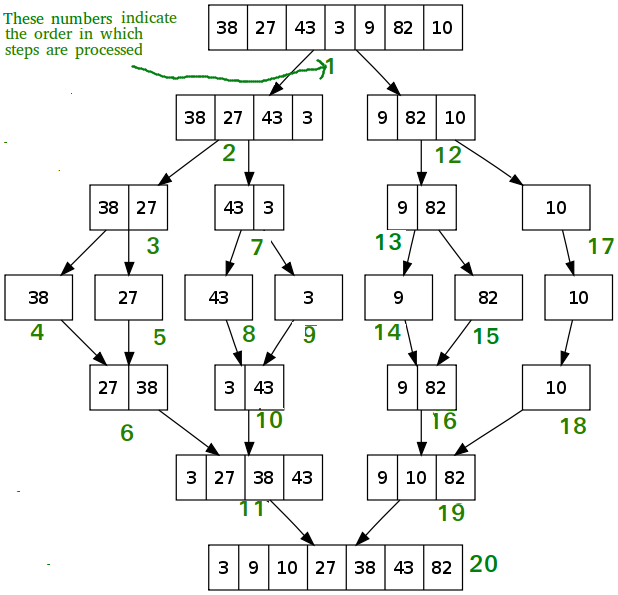
퀵 정렬(Quick Sort)처럼, "분할 정복(Divide and Conqure)" 알고리즘이다
병합 정렬은 인풋된 배열을 절반으로 나누고, 재귀함수로 하나의 요소가 남을 때까지 계속 나눈다
그런 다음 정렬을 하며 병합한다
Merge(arr, l, m, r) 함수는 나눠진 두 배열arr[l..m], arr[m+1..r]을 정렬하고 병합시키는 데에 사용된다
- Stable Sort
-GeeksforGeeks
Time Complexity:
병합 정렬은 재귀 알고리즘이기 때문에 시간 복잡성은 재귀 상태(recurrence relation)에 따라 증가할 수 있다
T(n) = 2T(n/2) + O(n)
...
- O(nlogn)
반응형
'Algorithm' 카테고리의 다른 글
| [C code] 원형 큐 (Circular Queue) (0) | 2020.01.07 |
|---|---|
| [C code] 퀵 정렬 (Quick Sort) (0) | 2020.01.07 |
| [C code] 버킷 정렬 (Bucket Sort) (0) | 2020.01.07 |
| [C code] 계수 정렬 (Counting Sort) (0) | 2020.01.04 |
| [C code] 삽입 정렬 (Insertion sort) (0) | 2020.01.04 |


