반응형
이항 계수 설명에 앞서, 동적 계획법에 대한 설명은 다음 게시글을 참고하자
[C code] 동적 계획법 (DP ; Dynamic Programming)
동적 계획법이란 복잡한 문제를 부분적인 문제(subproblem)로 나누어 푸는 방법을 말한다 예를 들어, 1번 줄에서부터 10번 줄까지의 어떤 조건에 따라 계산을 하는데 2번 줄에서의 계산 방식과 7번
snupi.tistory.com
이항 계수
이항 계수란, n개의 물건에서 중복을 허락하지 않고 k개를 꺼내는 조합의 수를 말한다
원래의 방법대로라면,
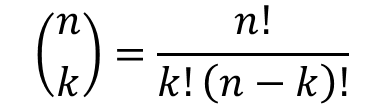
로, factorial(int n)의 함수를 구현하여, 계산할 수 있다
하지만 n, k값이 조금만 커지더라도 이 값을 구하기 매우 어렵다
따라서 다음과 같은 성질을 이용하여 값을 구해야한다
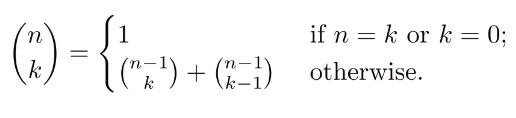
이와 같은 점화식을 보았을 때, 동적 계획법을 사용한다는 감이 올 것이다
코드는 다음과 같다
#include <stdio.h>
#include <stdlib.h>
int min(int a, int b)
{
if(a<b)
return a;
else
return b;
}
int bin(int n, int k)
{
int dp[n+1][k+1];
for(int i=0 ; i<=n ; i++)
for(int j=0 ; j<=min(i, k) ; j++)
{
if(j == 0 || j == i)
dp[i][j] = 1;
else
dp[i][j] = (dp[i-1][j] + dp[i-1][j-1]) % 10007;
}
return dp[n][k];
}
int main()
{
int n, k;
scanf("%d %d", &n, &k);
printf("%d", bin(n, k));
return 0;
}
dp[n+1][k+1]의 메모리를 선언한 후, Bottom-Up 방식으로 값을 채워나간다
반응형
'Algorithm' 카테고리의 다른 글
| [C] 트리 회전 (0) | 2020.12.16 |
|---|---|
| 온라인 알고리즘 / 오프라인 알고리즘 (0) | 2020.12.13 |
| [Python] 유클리드 알고리즘 (0) | 2020.12.10 |
| [C] 삼분 탐색(Ternary Search)과 이진 탐색(Binary Search) (0) | 2020.12.08 |
| [C] 소수 판별하기 / 에라토스테네스의 체 / 소인수 분해 (0) | 2020.12.08 |
