회전하게 되는 경우에 대해서 먼저 정의를 해보자. 총 4가지 타입으로 나눌 수 있다. 새로 삽임된 노드 N으로부터 가장 가까우면서 균형 인수가 +-2가 된 조상 노드를 A라고 하자.
-
LL 타입 : N이 A의 왼쪽 서브 트리의 왼쪽 서브 트리에 삽입된다. (Left Left)
-
LR 타입 : N이 A의 왼쪽 서브 트리의 오른쪽 서브 트리에 삽입된다. (Left Right)
-
RR 타입 : N이 A의 오른쪽 서브 트리의 오른쪽 서브 트리에 삽입된다. (Right Right)
-
RL 타입 : N이 A의 오른쪽 서브 트리의 왼쪽 서브 트리에 삽입된다. (Right Left)
LL과 RR은 대칭이고 역시 LR과 RL도 대칭이다. 이제 각 타입별로 알맞게 트리의 균형을 맞추자. 다음은 각각의 경우 대하여 균형 트리로 다시 만드는 방법이다.
-
LL 회전 : A부터 N까지의 경로상의 노드들을 오른쪽으로 회전시킨다.
-
LR 회전 : A부터 N까지의 경로상의 노드들을 왼쪽-오른쪽으로 회전시킨다.
-
RR 회전 : A부터 N까지의 경로상의 노드들을 왼쪽으로 회전시킨다.
-
RL 회전 : A부터 N까지의 경로상의 노드들을 오른쪽-왼쪽으로 회전시킨다.
한번만 회전시키는 것을 단순 회전(Single rotation)이라고 하는데 LL 회전, RR 회전이 여기에 속한다. 이 경우, 탐색 순서를 유지하면서 부모와 자식의 위치를 교환하면 된다. 두 번의 회전이 필요한 것은 이중 회전(Double rotation)이라고 하며 LR회전, RL 회전이 여기에 속한다.
LL 회전

LL 회전
위 그림의 왼쪽 트리는 LL 타입의 경우로, 노드 6은 균형 인수가 2로서 불균형하다. 오른쪽으로 "회전"을 시키면(6과 5를 바꾸면) 다시 균형 트리를 만들 수 있다. "회전"은 루트와 자식 노드를 바꾸는 것을 의미한다.
보다 일반적인 경우를 생각해 보자. 일반적인 LL 타입은 조상 노드의 A의 왼쪽 서브 트리의 왼쪽 서브 트리에 노드가 추가됨으로 해서 발생한다. 다음 그림처럼 LL 회전은 노드들을 오른쪽으로 회전시키면 된다.

이 연산을 코드로 구현하면 다음과 같다.
// LL 회전
Node* rotateLL(Node* node) {
Node* leftChild = node->leftChild; // B 설정
node->leftChild = leftChild->rightChild; // T2 설정
leftChild->rightChild = node; // A 설정
setHeight(node); // 회전 이후 높이 다시 계산
return leftChild;
}
RR 회전
왼쪽 회전의 경우 트리를 왼쪽으로 한번 회전하면 균형을 맞추게 된다.
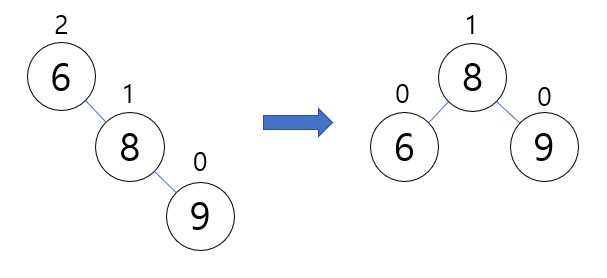
RR 타입은 조상 노드 A의 오른쪽 서브 트리의 오른쪽 서브 트리에 노드가 추가됨으로 해서 발생한다. 일반적인 경우의 RR 타입은 다음 그림처럼 노드 A와 B의 위치를 바꾸어 주고 서브 트리들을 정리하면 균형 트리가 된다.

코드로 표현하면 다음과 같다.
// RR 회전
Node* rotateRR(Node* node) {
Node* rightChild = node->rightChild; // B
node->rightChild = rightChild->leftChild; // T2
rightChild->leftChild = node; // A
setHeight(node); // 회전 이후 높이 다시 계산
return rightChild;
}
RL 회전

RL 타입은 그림처럼 조상 노드 A의 오른쪽 자식의 왼쪽 서브 트리에 노드가 추가됨으로 인해 발생한다. RL 회전은 균형 트리를 만들기 위해 2번의 회전이 필요하다. RL 회전은 LL 회전을 한 후, RR 회전을 하면 된다.
다음은 RL 회전 함수이다. 앞에서 구현한 단순 회전 함수를 호출하여 사용한다.
// RL 회전
Node* rotateRL(Node* node) {
Node* rightChild = node->rightChild;
node->rightChild = rotateLL(rightChild);
return rotateRR(node);
}
LR 회전

LR 타입은 그림과 같이 A의 왼쪽 자식의 오른쪽 서브 트리에 노드가 추가됨으로 해서 발생한다. LR 회전은 균형 트리를 만들기 위하여 2번의 회전이 필요하다. LR 회전은 RR 회전을 한 다음, LL회전을 하면 된다.
다음은 LR 회전 함수이다.
// LR 회전
Node* rotateLR(Node* node) {
Node* leftChild = node->leftChild;
node->leftChild = rotateRR(leftChild);
return rotateLL(node);
}
출처 :
- velog.io/@underlier12/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%ED%95%99%EC%8A%B5-11-ytk5nzm3m2
-https://lipcoder.tistory.com/entry/AVL-트리
'Algorithm' 카테고리의 다른 글
| [Python] KMP 알고리즘 (문자열 검색 알고리즘) (0) | 2021.01.05 |
|---|---|
| [C] 우선순위 큐와 힙 (priority queue / heap), 힙 정렬 (Heapsort) (0) | 2020.12.19 |
| 온라인 알고리즘 / 오프라인 알고리즘 (0) | 2020.12.13 |
| [백준 11051번][C] 이항 계수 (동적계획법 ; DP) (0) | 2020.12.13 |
| [Python] 유클리드 알고리즘 (0) | 2020.12.10 |


